どうも、りきぞう(@rikizoamaya)です。
大学院では、キャリア論と社会保障を研究していました。
社会人なってからは、予備校講師 → ウェブディレクター → ライターと、いろんな職業にたずさわってきました。
働き方についても、契約社員 → 正社員 → フリーランスと、ひと通り経験してきました。
働くなかで思うのは、自分の市場価値をアップするには「教養」が大切だということ。
「発想がすごいなぁ」
と、思う人は、キホン、教養を身につけています。
これまでたくさんの古典・学術書を読みあさってきました。
あらためて「核となる知識」をマスターしていきたいと考えています。
ここでは「代表的な古典」&「教養ワード」を紹介していきます。
哲学&経済学から、ビジネスや仕事に役立つ知識を共有していきます。
今回とりあげるのは、
です。
そのなかでもとくにキホン的な「変数」「曲線」「傾き」についてのべていきます。
経済学にかぎらず、グラフは、さまざまな記事やレポートで活用されます。
なにげなくみていますが、意味もわからず、テキトーに理解している場合が多いですよね。
うえのワードから、グラフの基礎を理解していきたいと思います。
以下、つぎのテキストを参考に、くわしく説明していきます。
引用のページは、こちらの本によります。
目次
グラフのキーワード
さまざまな種類がありますが、グラフはつぎの3つをおさえておけば、ざっくり理解できます。
- ① 独立変数 / 従属変数
- ② 線形関係 / 非線形関係
- ③ 曲線の傾き
以下、くわしくみていきます。
① 独立変数 / 従属変数
変数(variable)とは、「2つ」以上の値をしめす数量のことです。
たとえば、「アイス3コ」とか「気温25度」など、「2」よりも多い数であわらすことができれば、すべて「変数」になります。
そのうえで、独立変数(independent variable)とは、ほかの変数を決定する数のことをさします。カンタンにいえば、影響をあたえる数のことです。
いっぽう、従属変数(dependent variable)とは、ほかの変数に決定される数のことをさします。カンタンにいえば、影響をあたえれる数のことです。
つまり、2つの変数のあいだには「因果関係」があるとわかります。
たとえば、「気温」を「独立変数」、「アイスの販売数」を「従属変数」におけば、「気温」と「アイスの販売数」に〝原因 → 結果のカンケー〟があるかわかるのです。
(ちなみに、かならず「因果関係」があるわけではありません。あくまで、その可能性があるということです。それを調べるのが研究(リサーチ)です。)
たいていのグラフは、変数のあいだの関係をしめす
経済学にかぎらず、たいていのグラフは、2つの変数を置きます。そのうえで、2つの関係性をあらわします。
というより、グラフで表示するメリットは、両者の関係性をわかりやすく伝えることにあります。
なので、ほとんどのグラフでは、独立変数 / 従属変数が示されます。
じっさいのグラフ
それでは、じっさいにグラフをみてみましょう。
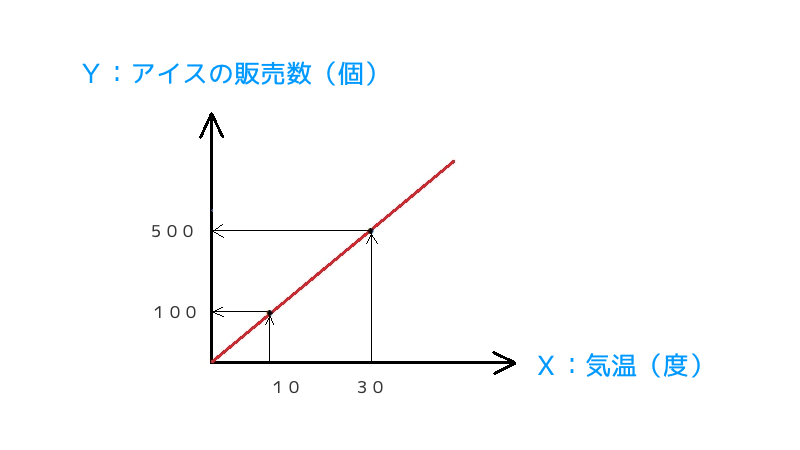
さきほどの例にならえば、こんなかんじになります。
横軸(X軸)に、独立変数である「気温」をおきます。
縦軸(Y軸)に、従属変数である「アイスの販売数」をおきます。
これによって、「気温」が「アイスの販売数」に、どんな影響をあたえているのかがわかります。
たとえば、気温が「10度」のときには、アイスの販売数は「100個」、「30度」のときには「500個」といったかんじです。
ちなみに、「お約束ごと」として、横軸(X軸)に「独立変数」をおき、縦軸(Y軸)に「従属変数」をおくのが、通例になっています。
決まりはありませんが、たいていはこうなっています。
② 線形関係 / 非線形関係
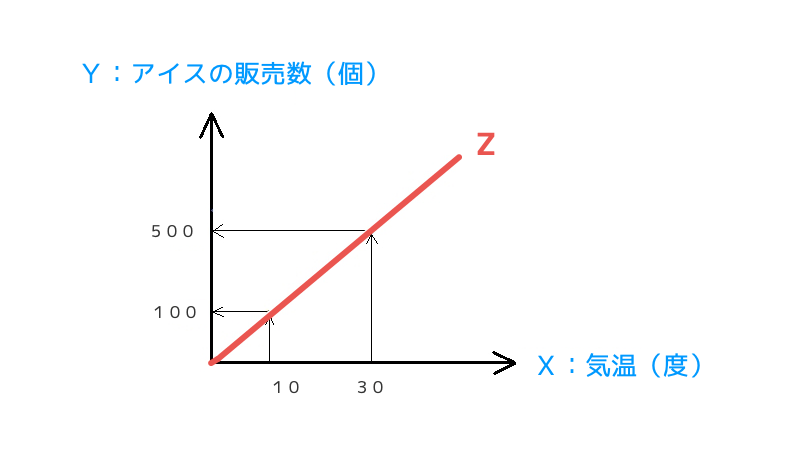
さきほどのグラフをみると、2つの変数が交差している点をつないだ線があります。
(かりに「Z」としておきます)
この線を「曲線(curve)」とよびます。
そのうえで、この線が「まっすぐ」の場合に、「線形関係(linear relationship)をもつ」と言われます。
いっぽう、この線が「曲がっている」場合に、「非線形関係(non-linear relationship)をもつ」と言われます。
また、この図のように、独立変数が1つ増えるごとに、従属変数もアップすれば、「正の関係をもつ」と言います。
たほう、独立変数が1つ増えるごとに、従属変数がダウンすれば、「負の関係をもつ」と言います。
曲線をみることで、2つの変数のあいだ、正負の関係がわかるわけです。
たとえば、
・それとも、気温が1度アップすれば、アイスの販売数は下がるのか
などなど。
曲線をみることで、2つのあいだの関係性がわかります。
ちなみに、「線形関係」のとき、線は「まっすぐ」に表示されますが、その場合でも「曲線」とよびます。
ちょっと、ややこしいですね。
③ 曲線の傾き
曲線の傾きとは、文字どおり、傾斜の程度をあらわします。
つまり、独立変数が従属変数に、〝どの程度の影響をあたえているか〟がわかります。
たとえば、うえの図のように、曲線(Z)が「まっすぐ」ならば、気温アップによるアイスの売れ方は「一定」とわかります。
しかし、曲線(Z)が、「ゆがんで」いれば、気温アップによるアイスの売れ方は「変動」しているとわかります。
たとえば、25度〜30度のあいだでは、1度アップにつき、「+30個」売れていたのが、30度〜35度のあいだでは、1度アップにつき、「+10個」しか売れないといったケースです。
線形関係の傾き
曲線が「まっすぐ」の場合、傾きはカンタンに求められます。
Yの変化(=従属変数)を、Xの変化(=独立変数)で、割ればいいからです。
公式であらわすと、こうなります。
x、yに、それぞれ数値をあてはめると、具体的な傾きの数(%)がわかります。
ちなみに、「Δ」とは、ギリシャ語の大文字で、「デルタ」とよみます。
非線形関係の傾き
非線形関係の傾きでは、独立変数 / 従属変数が交差する点を移るにつれて、傾きが変化する線のことです。
そのうえで、はじめは「ゆるやかな」な傾斜で上がっていたのが、とちゅうから傾斜が「急になる」場合、
とされます。
クルーグマンのテキストから引用すれば、こんなかんじです。
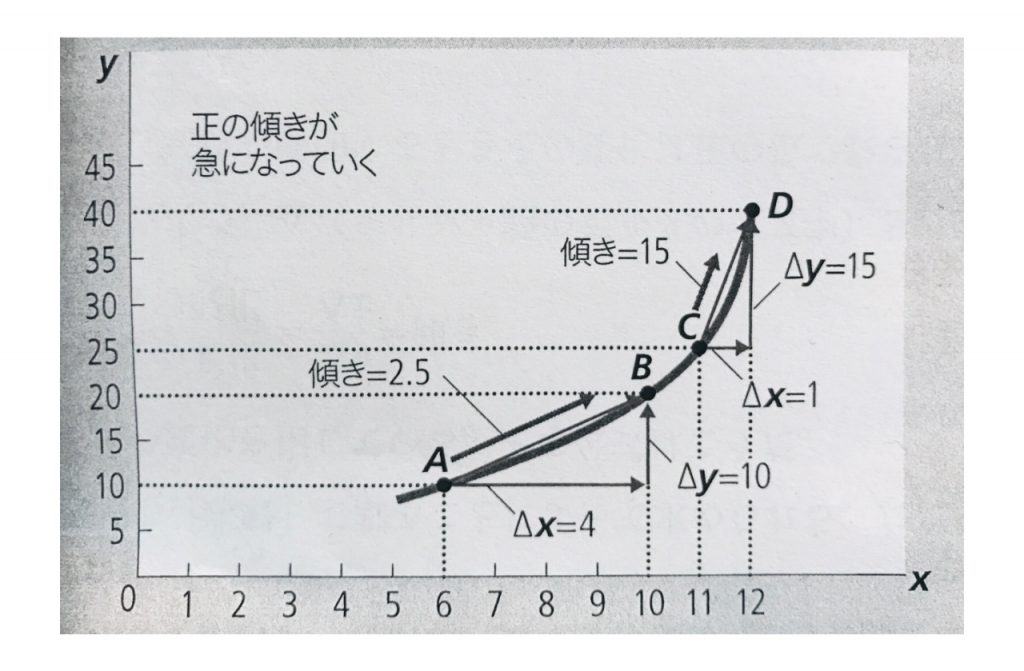
いっぽう、はじめは「急な」傾斜で上がっていたのが、とちゅうから傾斜が「ゆるやかになる」場合、
とよばれます。
同じく引用すれば、こんなかんじになります。
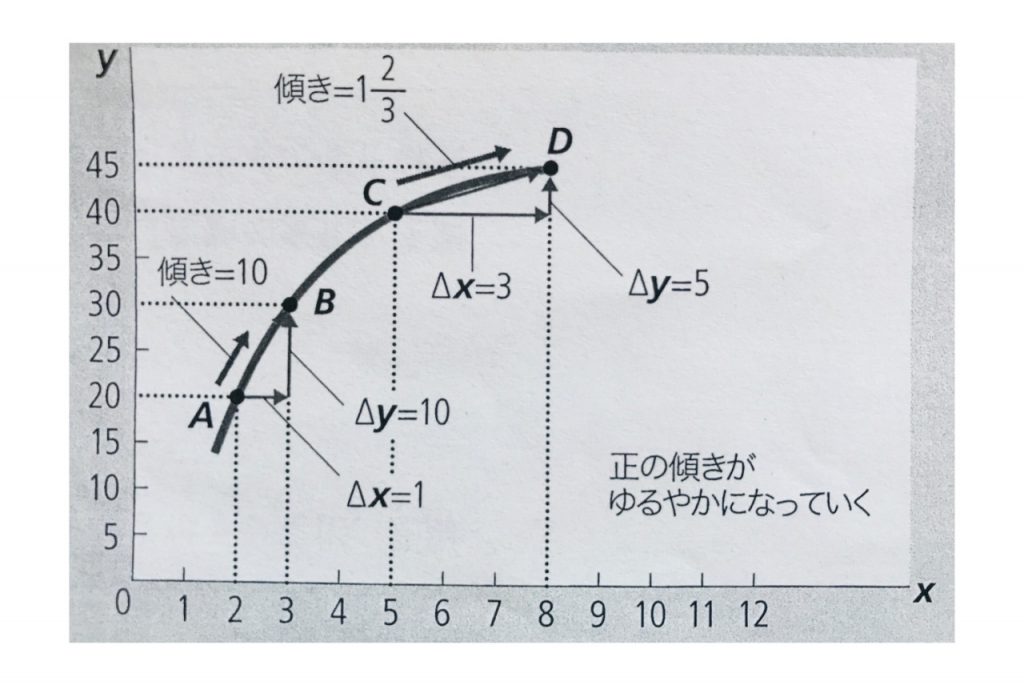
これは逆のケースも同じです。
はじめは「ゆるやかな」な傾斜で下がり、とちゅうから傾斜が「急になる」場合、
とよばれ、
はじめは「急」な傾斜で下がり、とちゅうから傾斜が「ゆるやかになる」場合、
とよびます。
おわりに
グラフをみる or 書くうえで、ポイントとなる要素をみてきました。
くりかえすと、
- ① 独立変数 / 従属変数
- ② 線形関係 / 非線形関係
- ③ 曲線の傾き
の3つです。
キホン、この3つのパーツから構成されています。
あとは、グラフをみるたびに、この3点を意識すれば、見るべきポイントがわかってきます。
経済学にかぎらず、グラフは、記事やレポートで、たびたび登場します。
また、プレゼンなどで、自分で書く場合も多くあります。
知っておいて、損はないと思います。
ここにあげた記事を参考に、あらゆるシーンで活用してみてください。
きょうあげた知識が、あなたの役立つとうれしいです。
ではまた〜。




